Our two major features in this issue of StarTuned are about alignment and ABS,  both of them affecting control of the car along the roadway. But round black rubber is the constant between everything on the car and the roadway, so let’s talk tires first.

Pressure and Traction There’s an optimal pressure for a given load. Below that and the treadpatch squirms while the sidewall overheats from flexing. Above that and you don’t get a full footprint. Conditions can shift this slightly: higher pressure will resist aquaplaning by reducing the treadpatch and thus increasing the pressure per square inch. Treadpatch area times pressure equals the load at that wheel, tossing in a little ‘fudge-factor’ for the stiffness of the rubber. Every variation in treadpatch area (from bumps and potholes) changes the pressure in the tire slightly, lifting the wheel if the pressure increases, lowering it if the pressure goes down.

Remember how your mind slumped into a yawning torpor when your teacher droned, “Today, class, we’ll review… again.” No reviews here. We won’t bore you with tire lore you already know, like the difference between bias-ply and radial tires, what ‘aspect-ratio’ means applied to tires, how water-shedding tread patterns reduce aquaplaning or the difference between static and dynamic wheel balance. No nagging about the importance of checking tire pressure or measuring tread depth, rotating tires regularly or fitting tires of the correct size and type. If you don’t already know all those things, learn and practice them before you do tire work on somebody’s car. But we hope most of this tire information is new, information to illuminate your thinking and help your work on alignment and ABS.

How Does a Tire ‘Work’?

The question seems odd because it looks like we can already see how a tire works. Doesn’t it just smooth out small bumps and keep the wheel from getting bent? Besides, there aren’t any moving parts to a tire. How can it ‘work’ at all? What is it the tire does?

A tire ‘works’ by performing several tasks on a vehicle. It provides enough traction to reel in the paint stripe between the lanes and to shove the scenery deep into the rearview mirror. It achieves the grip to keep the road under the drivetrain and the car’s shiny side up. But that’s not the tire’s first job. If you just put a brand new set of tires on the wheels and bolt the wheels up to the hubs, the weight of the car will rest solidly on the ground. Tires don’t hold the car up; compressed air does.

Let’s start at the beginning, with the tire’s work hoisting the car’s weight and the tire’s most important component, that ring of compressed air. Almost everything in the car rests on some other component, the way the engine rests on the engine mounts, which in turn rest on the subframe and suspension. The driver rests on the seat, and the seat on the floor and frame channels. The car’s entire body and powertrain weight rests through the suspension on its four wheels. One thing stacks atop another from the roof down to the wheels.

But unless a tire is deflated flat and its wheel rests on the pavement through the folded tire rubber, the wheels don’t rest on anything. Instead, the wheels hang in the eight loops formed by the beads of the four tires, two apiece. These loops are, in almost every tire, multistrand steel cables. The beads are slings, loaded in suspension, not in compression. The weight of the car, supported on the wheels in the tire beads, hangs just like a suspension bridge from its cables. If the car weighs 4000 pounds, thus, each tire’s beads hold about 1000 pounds. The beads are actually much stronger than that to accommodate shock and stress loads occurring under severe impacts.

Then what holds up the tire beads? The belts in and over the top half of the tire. We don’t ordinarily put an intact but deflated tire on a wheel, bolt that to an axle flange, lower the car to the ground and only then inflate the tire. But if we did, the pneumatic hoisting mechanism would be clearer. The increasing air pressure applies in all directions with equal force to every square inch on the inside of the tire and the wheelrim. The pressure around the wheelrim increases as the inflation goes up, but it does so equally all around its perimeter and all across its width. Since the inflation pressure on the wheel itself is equal all around, that can’t possibly contribute to lifting the weight of the car and so it doesn’t explain how the compressed air lifts the car.

If not pressure on the inside of the wheelrim, then it must be the pressure against the inside surface of the tire, because that’s all that’s left. The surfaces of the sidewalls hold about half a ton of pressure pushing outward each way, locking the beads against the rim, sealing in the air. But sidewall pressure pushes out, sideways, not up. That leaves only the pressure around the tread, inside the belts.

Nitrogen Inflation Here’s a bit of inflation lore you might have heard and something about how realistic it is. Car racing teams usually inflate their tires with nitrogen rather than with compressed air. About 80 percent of air is nitrogen, anyway, so this is not a particularly radical measure. The idea is to eliminate as much as possible any moisture in the inflation gas. All inflation gas, including pure nitrogen, will lose or gain pressure with temperature, following Boyle’s Gas Law, but gradually and predictably. Double the temperature while holding the volume constant, and you double the pressure. Reduce the temperature, and you reduce the pressure proportionate to the absolute temperature change. The humidity inside the tire does make a difference because it can mean the tire pressure fluctuates more with temperature than you’d like and at abrupt thresholds. Here’s how it works: Humidity is a function of temperature – the higher the temperature of the air, the more water vapor it can hold in solution. As the air cools, it eventually reaches the “dewpoint,” the combination of temperature and humidity when the water vapor reaches full saturation (100 percent humidity) and starts to precipitate out as liquid water. In volume, it takes a lot of vapor to make up a relatively small volume of liquid water. When you remove that water-vapor volume from the inflation gas, the pressure drops more than the temperature change alone would cause. The practice derives presumably from aircraft tires, which have used almost pure nitrogen for a long time. When an airliner reaches cruising altitude, the temperature of the air in the wheelwells may be below zero. But if the tires had been inflated with very humid air, the moisture would have precipitated out of solution, liquefied and frozen in the tires. Since it’s unlikely any ice in the tires will thaw and revaporize by touchdown, that could mean in the extreme case a dangerously reduced tire pressure at the very moment you want it to be perfect. Evidently water vapor dissolves more readily in oxygen than in nitrogen, so by excluding the oxygen you can avoid the moisture/change-of-phase problem. What does this mean in your shop? Should you rush out and get nitrogen tanks? Probably not. It won’t hurt to use nitrogen, but it’s not going to do any measurable good, either. Car tires don’t spend hours motionless at subzero temperatures and then suddenly sustain a smoking, full-load compression shock while spinning up beyond 150 mph at the same instant. Keep your compressor tank drained dry, and you won’t have enough moisture in the inflation air that this will be a real-world problem. Your pneumatic tools will last longer, too.

The pressure around the tread is equal, too, so how can it lift weight when the same pressure against different places inside the same wheel and tire could not? Pressure around the tread and along the sidewall also pulls the bead outward in all directions – but not equally in all directions. The difference around the tread is that the pressure on the bottom, the pressure just opposite the part of the tread currently touching the pavement, the treadpatch, encounters equal and opposite pressure upward from the road surface. The pavement, in fact, bends the naturally curved treadpatch flat, in an area corresponding directly to the load and the inflation pressure. Pressures above and below that roadpatch cancel out, and so the pressure under the belts at the top of the tire lifts the beads, wheels, car and all.

The air pressure around the circumference of the tire, just below the steel belts, also pulls the radial belts outward, thus pulling the beads outward. Of course the belts and beads are steel and don’t stretch under tire inflation pressure. But that equal and opposite counterpressure from the pavement unloads the pavement/treadpatch section of the tire. The air pressing down and the pavement pushing up squeeze the rubber and that part of the steel belt, of course, but that sector’s contribution disappears from the force applied through the radial belts to the lowest section of the beads. So the beads at the bottom pull down with less force than the beads at the top pull up, with in fact exactly the same force the treadpatch places on the road. The car’s weight hangs by suspension from the tire beads, which rest by compression on the air at inflation pressure on the top section of the tire. The air, in turn, constrained in the ring-space within the tire, presses against the displaced section of the treadpatch directly in contact with the pavement.

Notice this is just like a suspension bridge, using the compressed air ring in place of the stone pillars. But the bridge isn’t going anywhere, and the car is. Instead of a rigid stone column, the air in the tire forms an elastic, flexible torus. This is the first and most active part of the vehicle’s suspension: The treadpatch follows the undulations of the pavement, but the undulations cause microvariations in the tire inflation pressure, pulses corresponding to the ripples in the pavement. The compressibility of the air and the elasticity of the rubber allow absorption and insulation of the quickest and smallest undulations of the pavement, movements that would otherwise make the vehicle ride intolerable. Ever ride on solid-rubber-tires?

So that’s how the tire lifts the car. Here’s how it cushions the ride: Very small road irregularities simply deflect the rubber surface at that point, with negligible effect on the ride. If the car encounters a bump up, first the tread deflects upward, reducing the volume of airspace in the tire and correspondingly increasing the momentary air pressure. The upward deflection also increases the area of treadpatch in contact with the pavement. Both of these effects increase the lift the upper part of the tire can exert to hoist the beads. The tire deflects upward, pulling up the wheel and the spindle. The spring compresses upward; the car rises at that corner. Just the opposite occurs when the car goes over a pothole or dip: the treadpatch loses area; the lift the upper part of the tire can exert on the beads drops correspondingly. The suspension extends, and the car dips.

Inflation pressure does push the sidewalls out, but that doesn’t hold the car up. Tire sidewalls are never farther apart than when squashed out in a deflated tire. When you re-inflate the tire, pressure on those spread-out sidewalls constantly increases up to normal pressure, but at the same time they move back inward.

Inflation presses the sidewalls against the rim with a force of about 1000 pounds on each side. The resulting friction holding the tire to the rim is usually more than sufficient, well beyond the torque that could be put out by the engine or braking system or absorbed by the road surface. However there have been some nonoriginal wheels, brightly plated all over with smooth, shiny chrome, including on the mating surface between the wheel and the tire bead. Whatever be said about the ‘lotsa-chrome’ decorator touch, it doesn’t belong between tire and wheelrim.

High-Speed Distortion One of the odder forms of tread behavior occurs at high speeds, when centrifugal force acting on the tire wants to make the tread circumference grow by centrifugal force. The steel belts are strong enough to prevent that from happening to any great extent, but there aren’t steel belts in the sidewalls. That means the sidewalls can lift upwards and increase the wheel diameter just at the shoulder of the tire, in what are called ‘pantographic effects.’ You can see how this could have unexpected traction results, as the center of the treadpatch developed less and less pavement contact at higher speeds. Modern high-speed-rated tires include auxiliary Kevlar- or Aramid-fiber belts right at the shoulder of the tire to constrain this kind of centrifugal-force growth.

It’s unlikely (absent the use of some sort of grease as a tire-mounting aid) the tire can turn much on a rim, even on such slick wheels, but it could move by an inch or so with hard braking or acceleration. And then another inch or so the next time. In an extreme case, that could throw off the wheel balance as well as any steps taken to minimize radial and lateral runout. You know, of course, about aftermarket wheels that block sufficient flow of air to keep the brakes cool under extreme circumstances. The advantage of sticking with a tire and wheel called out in Mercedes-Benz specifications is that you can have a high level of confidence there won’t be any functional shortcoming masked as ‘styling’ that slipped past their testing.

We’ve discussed how the tire holds the car up because a similar mechanism controls the car underway, and understanding how it works clarifies ABS and alignment diagnosis and work. The belts, tensioned by the inflation pressure, conduct all the directional forces between the treadpatch and the wheel.

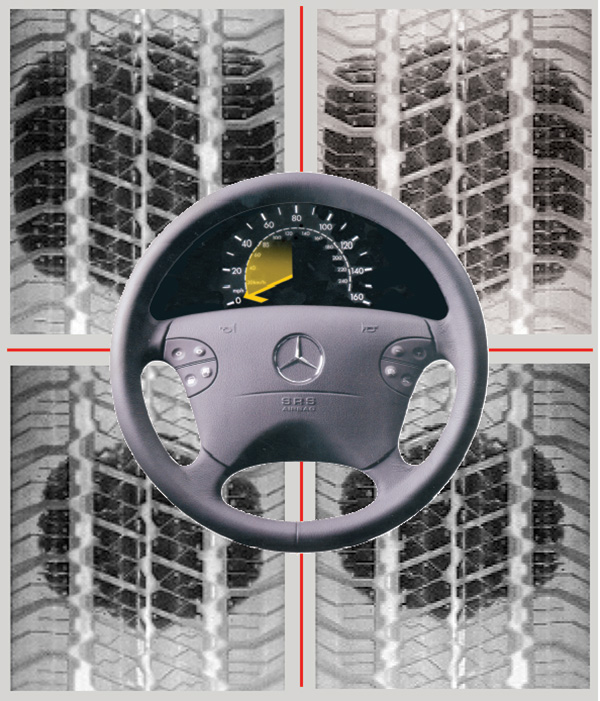
Let’s look at five sets of remarkable treadprint photos provided to StarTuned by Goodyear, evidently taken under their glass-road test facility. These cover steady, straight-line driving, accelerating, braking, turning left and turning right. We can see what’s going on at each of the four wheels in these circumstances. Please keep in mind these are tire graphics, not car photos. We have no way of telling what kind of vehicle was used for the tests or even whether the tires shown are specified for any Mercedes-Benz vehicle at all. There’s every reason to suppose the treadprint variations are representative of all cars, however.

Straight ahead, steady speed. Assuming the inflation pressures are identical for all four tires, we see there is slightly more weight on the front tires than on the rears, typical for front-engined cars. There appears to be slightly negative camber on the front tires, as the inboard part of the treadprint shows a bit longer shoulder contact than the corresponding outboard section. I think this is so of the rear tires, too, but I’m less confident there. Slightly negative camber all around improves roadholding for most cars, as long as you stay within specs. The photos show no sideslip, and the water grooves are directly parallel to the direction of travel, represented by the edges of the photos. In these and all the other tireprint images, the tread bends flat abruptly just as it touches down and again as it lifts. At the same time and unseen here, the sidewalls flex at just the space of contact. This flexing as well as friction during turns, acceleration and braking, raises the temperature of the tire rubber. Left turn, constant speed. This and the next set of pictures show hard, but not white-knuckled turns. Most of the weight has shifted to the right wheels by centrifugal force; there’s almost no load on the inboard left shoulder. Each of the tires carries most of the weight on its right side, indicating that the force of the turn has forced the tire to roll away from the outboard sidewall. I would conjecture – but do not know – that Benz suspension geometry would show somewhat less of this ‘camber’ effect. We do see the beginnings of sideslip here, though. If the front wheel centerline points, let’s say, 10 degrees left of the car’s centerline, the tire treadpatch centerline will follow a line somewhat outboard of that, say 5 degrees. The tire twists under the wheel from the force of the turn. The centerline of the tread sets down close to the centerline of the tire, but as the car passes over it, leaning outward in the turn, the pavement progressively pulls the treadpatch back toward the center of the car. Right turn, constant speed. We notice, in the opposite direction, all the things we saw in the left turn. We also notice (as with the left) that the sideslip of the rear wheel is less than the front wheel sideslip. Reasonable design requires this, not only to achieve predictable handling, but also to keep the rear wheels grabbing pavement beyond the point when the fronts have lost it. Disconcerting as understeer can be in an emergency, it’s inherently far safer than the sudden spin of oversteer. With each of these sets of turning photos, you can also understand the consequences of braking and turning at the same time. In the absence of an ABS system, that combination could shift so much weight to the outside front wheel and remove so much from the inside rear, that a spin could become unacceptably likely. Straight ahead, braking. Again we see the weight-shift from a speed change. The front treadpatches have now grown larger than they were in steady cruise. We can also see the suspension of this car is sufficiently sophisticated that there is no detectable change of toe with the deceleration. In fact, we can’t even guess whether the car uses antidive/antisquat suspension geometry, because you’d still have the same change of treadpatch area with acceleration and deceleration. That change of area, directly proportionate to the shift of weight and correspondingly to the traction available, vividly shows why every vehicle needs some sort of proportioning function to the rear-wheel brakes: Should the rear wheels lock up, there’d be nothing to control the vehicle’s direction. Yaw change could be instantaneous and uncontrollable. Similarly, you’d never want enough front braking power and traction to bring about a 100 percent weight-shift, lifting the rears clear of the road. That would have the same effect. Braking also can cause the tire to wind more tightly on the wheel, effectively reducing the rolling diameter. Straight ahead, accelerating. We immediately notice the weight-shift to the rear tires, evidenced from the increase in the relative size of the rear treadpatches. Since the total weight of the car doesn’t change, however, the total area of all four treadpatches remains the same. This test did not involve accelerating enough to spin the rear drivewheels, but if it did, we’d see the separation of road and tire beginning at the back of the patch where there is the highest rubber stress. You’ve probably seen high-speed photographs of drag-racer tires as they wind tighter on the hub under power. The windup means the radial belts drive the wheel (and thus car) forward. It also means the wound-up belts lift the slipping, high-stress rear area of the treadpatch sooner than a normal, moderate acceleration would.

There’s an interesting traction anomaly that occurs in a steep sideslip (we’re only considering a car without any form of traction control here), interesting, that is, if you do alignments. Consider the extension of the caster axis to the point at which it intersects the pavement. Under most circumstances, this point is somewhat forward of the centerpoint of the treadpatch, and caster functions to pull the steering to the center. In a sideslip, however, the centerpoint of the treadpatch angles outboard of the wheel centerline, because the centrifugal side-load forces the tire to twist, just as we saw above. The stress on the treadpatch is greatest where the displacement is greatest, at the back edge. When a wheel starts to sideslip, most of the slip is at the back (as well as most of the tire wear).

Different tires are capable of different levels of slip, but 12 degrees is not unusual. The tire can continue to a higher angle of slip, as more and more of the treadpatch breaks loose from the pavement. But at a certain amount of slip, so much of the back of the treadpatch has broken loose that the caster angle axis now intersects the center and then the rear of the functional (i. e., non-slipping) contact patch. At that point, the steering is no longer self-correcting; there’s no more ‘caster’ effect. The wheel instead of requiring the driver to positively turn in the direction he wants to go, suddenly falls neutral and then wants to go all the way into the turn, past the position the driver wants. But before the steering can slam against the stop, the tirepatch breaks completely loose from the pavement, steering goes neutral again, and there is effectively no traction at that wheel. The car has literally gone ballistic, and trajectory physics, not steering, determines where it goes and when it stops.

While that can happen with the last degree or so of steering wheel angle, once the tire slips that much, you can’t recover traction by simply backing up that last errant degree. You have to countersteer hard, to bring the wheel centerline (and that of the tire) parallel to the direction of travel, perhaps 25 or 30 degrees toward the outside of the turn, away from the angle it held a fraction of a second before, away from the direction you want to go. Like driving an old car on black ice, not much of this is instinctual. You can understand why Mercedes-Benz went on to develop the ESP and other traction control systems we’ll cover in future issues.

StarTuned would like to thank Goodyear for some of the information in this article.